The n-vector page
Position calculations – simple and exact solutions by means of n-vector
n-vector is used to replace latitude and longitude, making the calculations simple and non-singular. Full accuracy is achieved for any global position (and for any distance).
This web page contains solutions to ten common geographical position calculations.
Background
Written by Kenneth Gade (PhD, Principal Scientist in the Navigation Group at FFI, Norwegian Defence Research Establishment).
For references, please cite:
Gade, K. (2010). A Non-singular Horizontal Position Representation, The Journal of Navigation, Volume 63, Issue 03, pp 395-417, July 2010.
Used worldwide for critical applications:
n-vector is used worldwide, e.g. for navigation, traffic control, and surveillance, of aircraft, cars, ships and submarines/submersibles. One example is Thales, who is world-leading at air traffic management (ATM). Their newest generation of ATM system is based on n-vector (replacing previous alternatives).
Solving ten common problems
We will now illustrate how ten common geographical position calculations can be solved using n-vector. The solutions are also available as Matlab code (and as C++, C#, Python, JavaScript, and other languages).
Color coding for figures and variables:
-
Input (red): The initial input that is given
-
Output (green): The solution to be found
Example 1: A and B to delta

Problem
-
Assume WGS-84 ellipsoid. The given depths are from the ellipsoid surface.
-
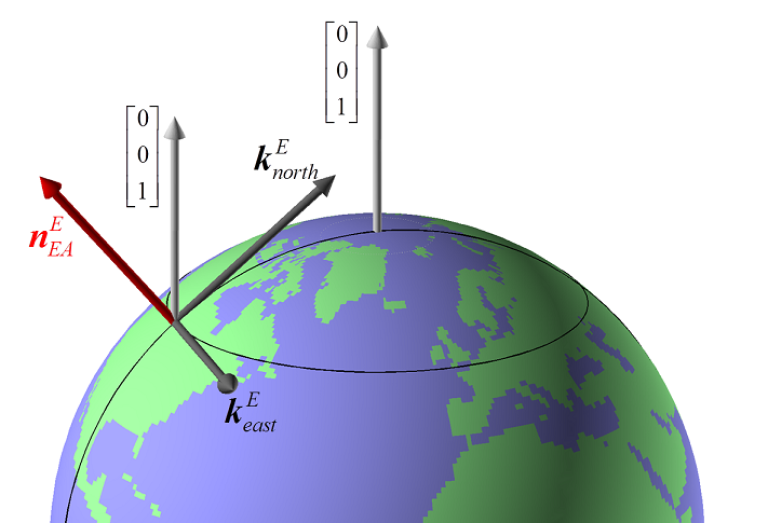
Use position A to define north, east, and down directions. (Due to the curvature of Earth and different directions to the North Pole, the north, east, and down directions will change (relative to Earth) for different places. Position A must be outside the poles for the north and east directions to be defined.
Solution
Example 2: B and delta to C
Problem
zyx2R.m).Solution
n_E2R_EN.m with n_E_and_wa2R_EL.m. See Table 2 in Gade (2010) and the help text in n_E_and_wa2R_EL.m for details.Example 3: ECEF-vector to geodetic latitude
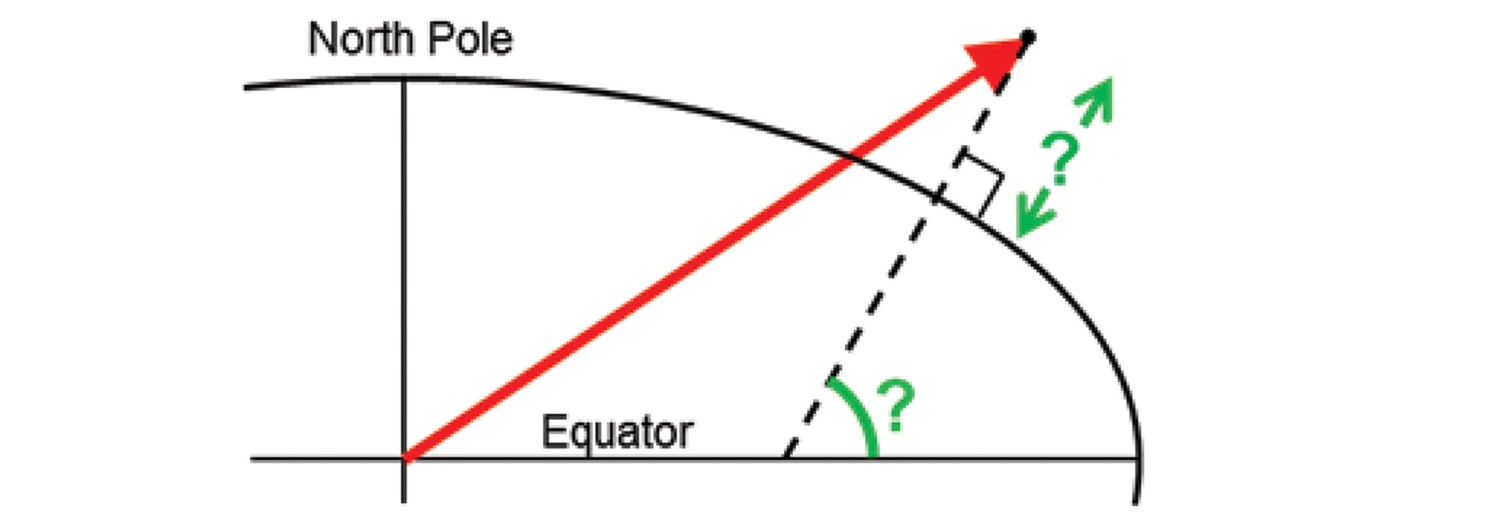
Problem
Solution
Example 4: Geodetic latitude to ECEF-vector
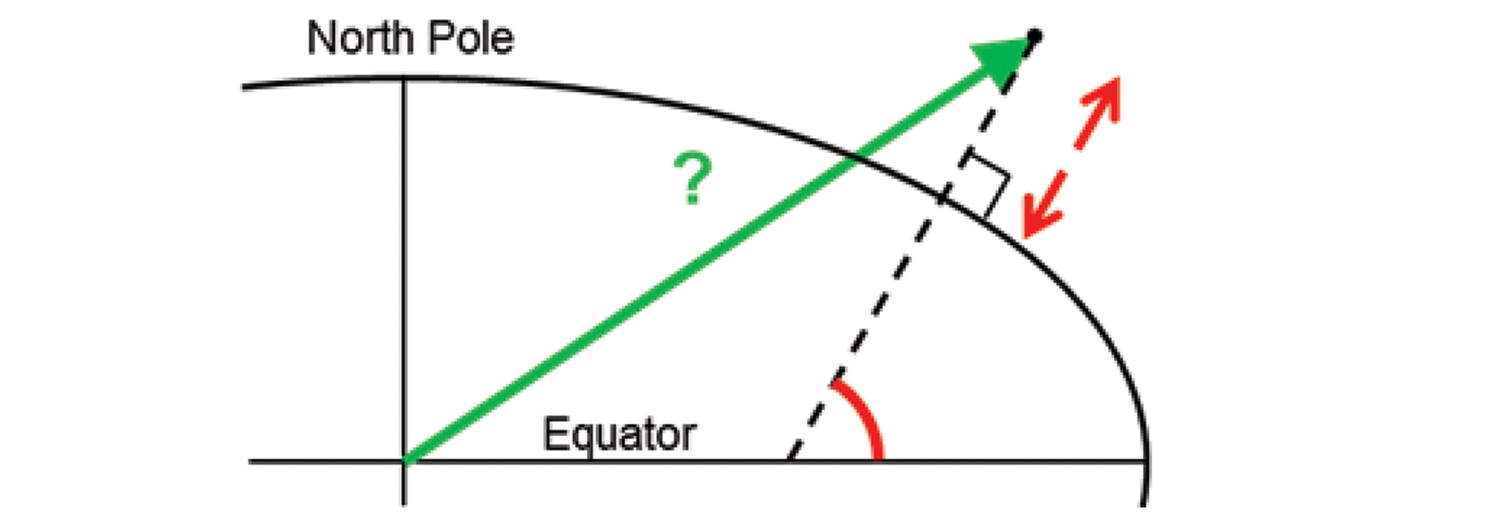
Problem
Solution
n_EB_E2p_EB_E.m. See also Appendix B in Gade (2010).In the remaining examples, we assume that a spherical Earth model is sufficiently accurate, and then the position functions used above are not needed. The examples demonstrate the simplicity of these calculations when using n-vector instead of latitude and longitude. The n-vector solutions are also non-singular for all Earth-positions and work across the Date Line (180th meridian).
Example 5: Surface distance
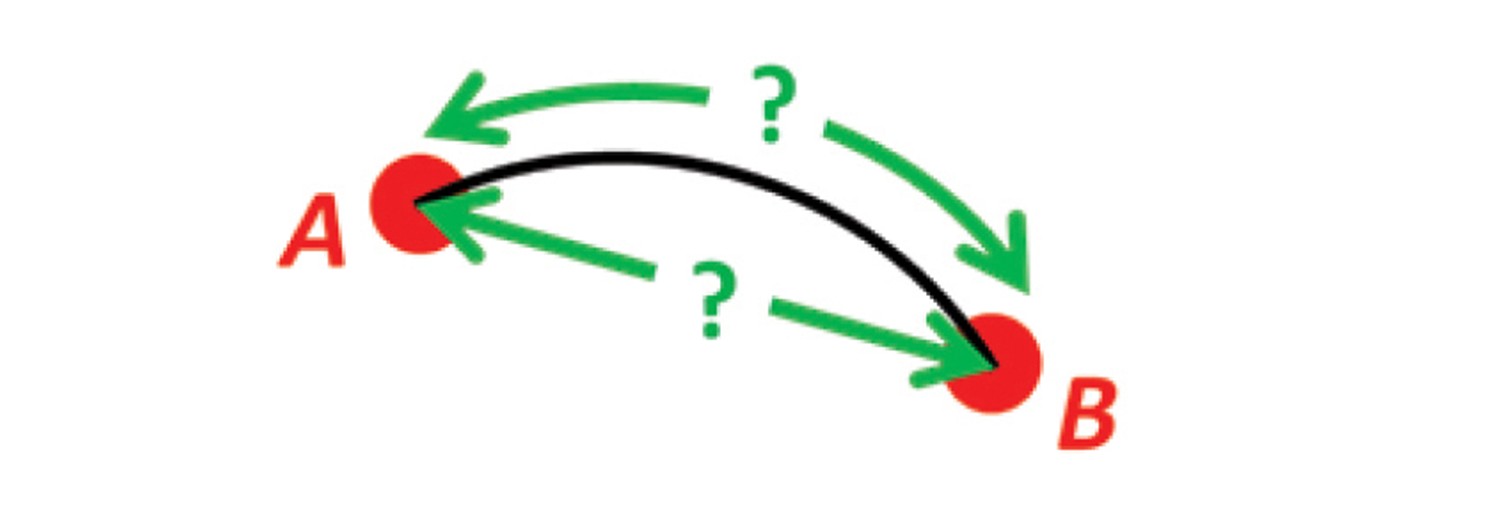
Problem
See vector symbols explained for more details about the mathematical notation.
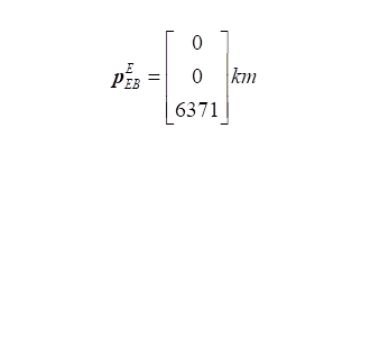
Given two positions A and B as
Solution
n_EA_E_and_n_EB_E2p_AB_E.m from Example 1, and take the norm of the output vector.Example 6: Interpolated position
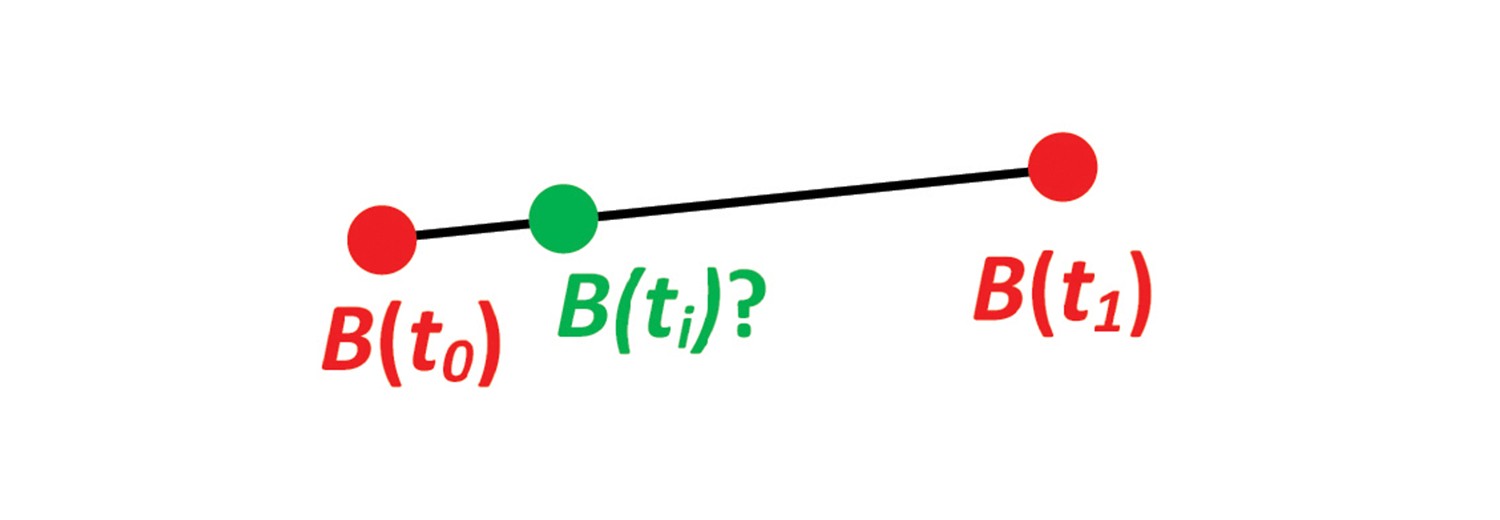
Problem
Solution
Example 7: Mean position/center
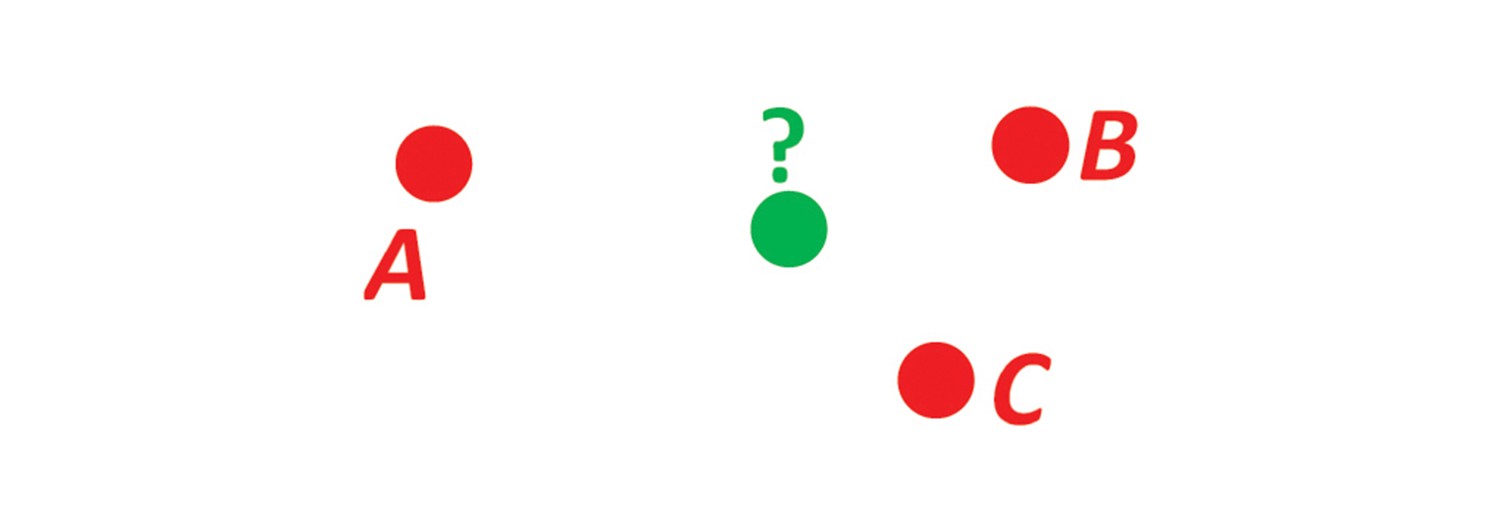
Problem 7
Solution 7
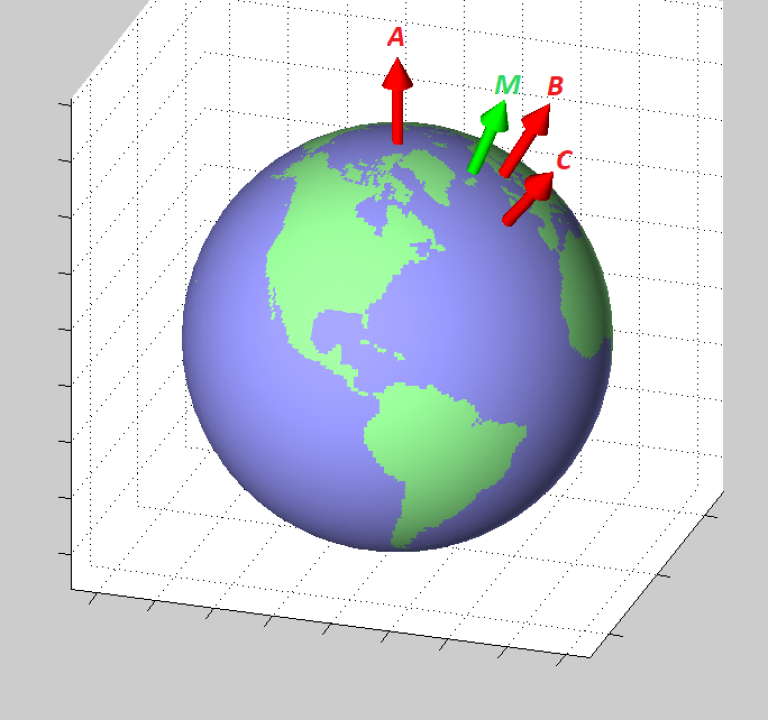
Details about the definition of the horizontal geographical mean position
Several definitions of a geographical mean/center/midpoint are possible. The solution given here can be described as the “center of gravity” of the given positions, and can be compared to the centroid of a geometrical shape. Informally, the found mean position can be described by the following: Assume a sphere that is a model of the Earth, and let the sphere roll freely on a horizontal plane (in a uniform gravitational field). Place weights at the given positions of the sphere, and the weights will pull one side of the sphere down due to the gravitation (assuming the positions are not antipodal). When the sphere is in equilibrium, the “center of gravity”-position is the tangent point between the sphere and the plane.
Another possible way to define a midpoint is the position where the sum of surface distances (great circle distances) from the original positions is at a minimum. This midpoint is undefined when only two positions are given. If three positions are given in one dimension as 0, 0, and 3, this midpoint is at 0, while the arithmetic mean is 1. Iterations are probably needed to calculate this midpoint, and code for this is not included at this web site.
Example 8: A and azimuth/distance to B
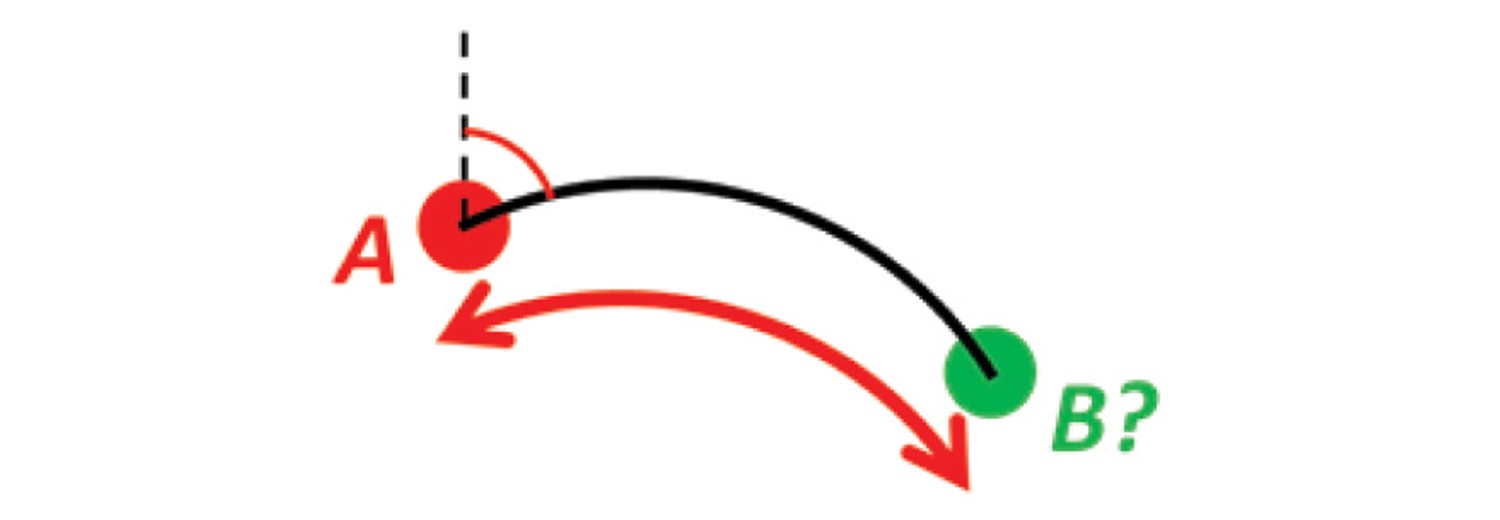
Solution 8


Example 9: Intersection of two paths / triangulation
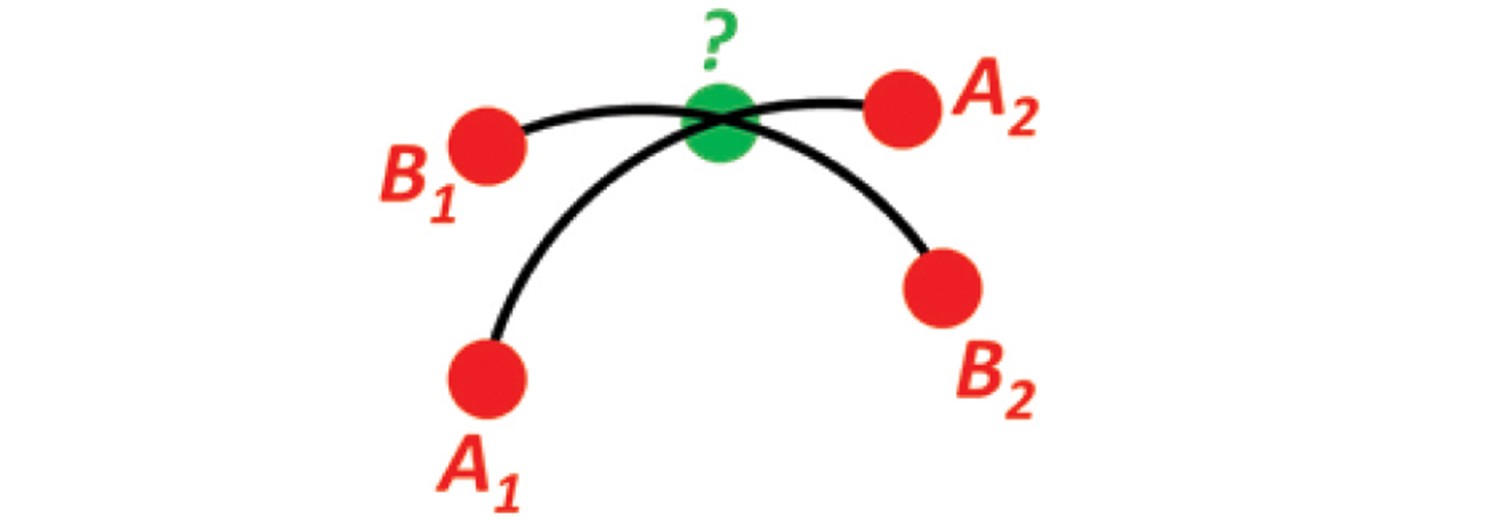
Problem 9
Solution 9
Example 10: Cross track distance (cross track error)
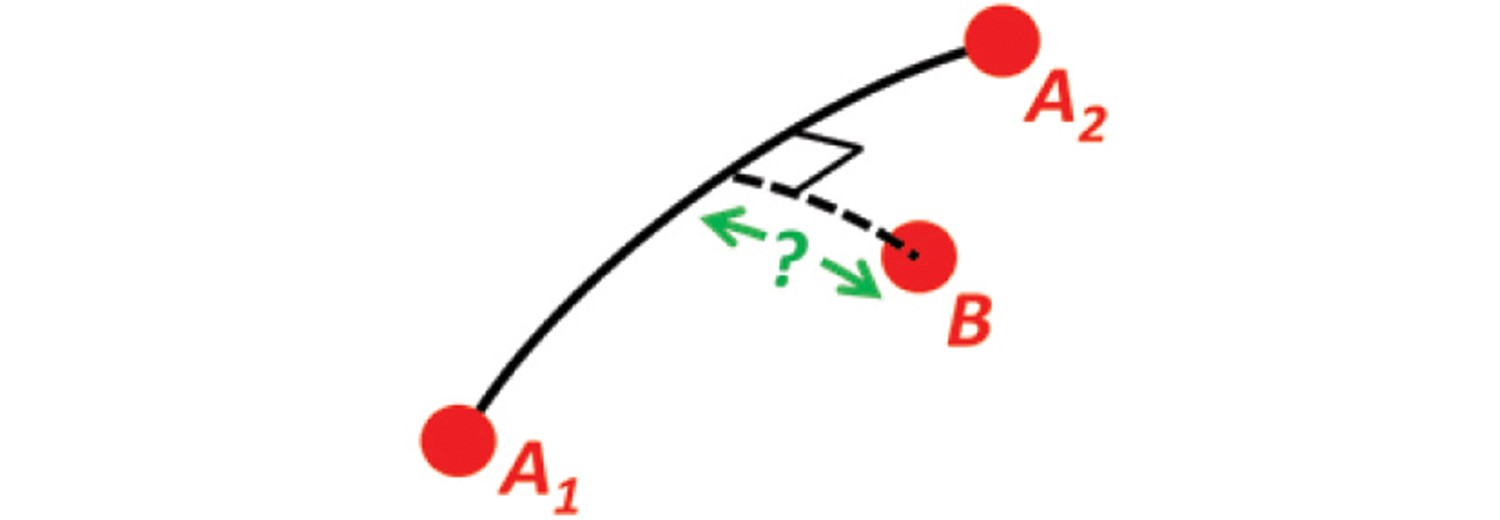
Problem 10
Solution 10

About the solutions
The four first examples are simply solved by using the functions provided for download. The functions are exact, and can use ellipsoidal or spherical Earth model. They are without iterations (i.e. on closed form), and WGS-84 reference ellipsoid is used as default. Custom ellipsoids/spheres can be specified. The functions are based on n-vector instead of latitude and longitude.
The last six examples are solved for spherical Earth, and then no functions are needed. Using n-vector instead of latitude and longitude, these examples are quite straightforward to solve by simple vector algebra.
The solutions to all 10 examples are non-singular, and they work equally well for all global positions (i.e. they work at the Poles, close to the Poles, and across the Date Line). The solutions also have full numerical accuracy for both short and long distances (they are numerically well-conditioned).