Hvor redd er kryptologene for kvantedatamaskiner?

Dagens kryptografi

Kryptografi kan enkelt sagt deles i to kategorier: symmetrisk og asymmetrisk. Dersom vi allerede er i en situasjon der to parter deler en felles hemmelighet (i denne sammenhengen teller det som symmetri), så kan de bruke den til å kommunisere sikkert. Dette er ikke stedet å gå i detaljer, men det er verdt å merke seg at Forsvaret fortsatt i stor grad distribuerer symmetriske nøkler, både fysisk og elektronisk.

De tidligste eksemplene på symmetrisk kryptografi går helt tilbake til de gamle grekerne, som surret lærreimer rundt staver med gitte størrelser, og skreiv på tvers av reima. Bare en mottaker med riktig stav kunne surre reima korrekt, og dermed lese meldingen. I dag bruker vi algoritmen Advanced Encryption Standard (AES) til omtrent alt. AES ble utviklet at belgierne Joan Daemen og Vincent Rijmen i 1998, og ble standardisert av USAs National Institute of Standards and Technology (NIST) i 2001, i sterk konkurranse med mange andre kandidater. 

I tillegg er vi avhengige av kryptografiske hash-funksjoner, som lager et kort – men forhåpentligvis unikt – fingeravtrykk av inndataene. Slike har blitt utviklet og standardisert på samme måte tidligere.

På internett er det sjeldent at vi faktisk deler en felles hemmelighet: Jeg har til gode å få en kurer fra Google på besøk for at jeg skal kunne bruke Gmail sikkert. Derfor må vi bli enige om nøkler fra nesten ingenting. Metoden for å gjøre det ble først publisert av Whitfield Diffie og Martin Hellman i 1976, og det er i hovedsak fortsatt deres idé vi bruker i dag. Når vi først har blitt enig om en felles hemmelighet, så har vi kommet oss i situasjonen over, og kan bruke AES eller annen symmetrisk krypto.

(Det er på dette stadiet jeg må ta konsekvensen av at det er to grupper av lesere. Noen av dere vet hva en syklisk gruppe er, og dere andre skal slippe å få det forklart. Her kommer derfor to forklaringer av Diffie-Hellman-nøkkelutvekslinga. Velg fritt.)

Den enkle: Diffie-Hellman baserer seg på en interessant matematisk struktur, der noen operasjoner er enkle å utføre, men veldig vanskelige å reversere. Dessuten ser disse operasjonene ut som om de er helt tilfeldige. Begge starter med et hemmelig tall for seg selv, og bruker denne i operasjonen. Så sender de resultatet av dette til hverandre, og gjør den operasjonen på nytt med det de får fra den andre. Da vil de ende opp med en felles hemmelighet, og ingen andre kan finne ut hva den er med mindre de greier å reversere operasjonen. Denne felles hemmeligheten kan de bruke til å lage nøkler.

Den matematiske: La G = (g) være ei syklisk gruppe av orden q og med generator g. Partene velger hver sine tilfeldige hemmelige tall a, b mellom 0 og q–1 og beregner A = g^a, B = g^b, og sender A, B til den motsatte parten. Dersom G er ei godt valgt gruppe, for eksempel ei undergruppe av den multiplikative gruppa av heltall modulo et primtall 2q + 1, eller ei undergruppe av de rasjonale punktene på en elliptisk kurve over en endelig kropp, så er det vanskelig å løse (blant annet) diskret logaritme-problemet. Da kan Alice beregne C = B^a og Bob C = A^b i gruppen, og de har en delt hemmelighet.

I tillegg brukes fortsatt systemet til Rivest, Shamir og Adleman (RSA) fra 1977. Det er basert på at dersom man har to store primtall p og q, og deres produkt n, så er det vanskelig å finne p og q om man bare har n. Det brukes i dag lite til å kryptere, men noen systemer bruker det til å lage signaturer, som bekrefter at en melding er sendt av den som skulle sende den. På den måten kan ingen uoppdaget utgi seg for å være nettbanken din. 

Dette kaninhullet er selvsagt mye dypere, men det ville blitt en lang digresjon. La oss komme oss opp igjen.

Kvantedatamaskiner

Enheten du leser dette på er veldig god til å behandle informasjon som enten er sann eller usann, 1 eller 0. Prosessoren kan behandle 64 slike bit om gangen, og det er nok til å betrakte langt større tall enn det de fleste av oss trenger i det daglige.

En kvantedatamaskin er derimot ikke så nøye på om det den regner på er helt sikkert 1 eller 0. I stedet bruker den kvantebits (qubits), som kan eksistere i en superposisjon mellom 1 og 0. Enkelt sagt kan de være begge deler samtidig, og hva de faktisk er, finner du først ut når du måler. I tillegg kan flere slike qubits flettes sammen, slik at målingen av én påvirker de andre også. Den vanligste (men heldigvis gale) måten å framstille dette på, er at en kvantedatamaskin kan betrakte alle mulige kombinasjoner av qubit-ene sine samtidig. 

Når man til slutt prøver å lese av tilstanden til en kvantedatamaskin vil qubit-ene kollapse til gitte tilstander av 1 og 0, og dersom du bare prøvde alle kombinasjoner, så ville du bare fått ut et tilfeldig og ubrukelig svar. Derfor må man bruke algoritmer som kan påvirke sannsynlighetsfordelingen disse qubit-ene følger, slik at den tilstanden vi leser ut til slutt faktisk er en løsning på problemet vårt.

I løpet av 1993 og 1994 kom Coppersmith og Shor med slike algoritmer. Coppersmith viste hvordan man kan bruke en kvantedatamaskin til å beregne Fourier-transformasjoner eksponensielt mye raskere enn en klassisk datamaskin kan gjøre det. Det er viktig fordi Fourier-transformasjoner igjen kan brukes til å gjøre multiplikasjon av store tall ekstremt raskt. Shor brukte dette til å lage en algoritme som vil løse akkurat de problemene som Diffie-Hellman og RSA er basert på, og det mye, mye raskere enn en klassisk datamaskin kan gjøre.

Så snart noen får til å bygge en kvantedatamaskin med tilstrekkelig mange qubits, så vil Shors algoritme (og de utallige forbedringene som har kommet i løpet av de siste 30 årene) gjøre at nøkkelutvekslingen på internett i dag blir nesten trivielt usikker. Game over?

Shors algoritme fungerer heldigvis ikke på AES og de hash-funksjonene vi bruker i dag, for de er ikke basert på de samme matematiske problemene. I 1997 kom Grover med en annen algoritme som lar en kvantedatamaskin finne den inndataen som vil gi en bestemt utdata fra en vilkårlig funksjon – for eksempel AES eller en hash-funksjon. Si at det er n (si, 100) mulige inndata til funksjonen. En vanlig datamaskin må prøve halvparten av disse før den har 50 % sannsynlighet for å ha funnet den riktige, og absolutt alle for å være sikker. Grovers algoritme lar en kvantedatamaskin gjøre det samme søket ved å bare sjekke (omtrent) √n (si, 10) ganger. (Jeg får litt vondt i hodet av akkurat den tanken.)

Grovers algoritme er langt mindre effektiv enn Shors algoritme. Konsekvensen er i teorien at nøkkellengdene til ethvert kryptosystem blir halvert, slik at en nøkkel på 128 bit får samme sikkerhet som om den bare var 64 bit. Men: Dette er bare i teorien. I praksis er det mye merarbeid som ikke gjenspeiles i det vi omtaler som asymptotisk kjøretid, slik at sikkerhetstapet i praksis er mye, mye mindre. Likevel – fordi det egentlig ikke koster noe særlig – har alle gått over til å bruke nøkler på 256 bit i AES. Det er mer enn nok til å være sikker mot kjente algoritmer på en kvantedatamaskin.

For å oppsummere hittil: Mot kvantedatamaskiner mister vi de vanligste algoritmene for asymmetrisk kryptografi som er i bruk i dag, mens de symmetriske algoritmene langt på vei er uberørt. Og, husk fra over hvilke algoritmer Forsvaret uansett bruker mest av i dag: de symmetriske.

Morgendagens kryptografi

Mosca har kommet med et slags meta-teorem: La x være tida det tar å bytte ut det siste systemet som bruker noe som er sårbart mot kvantedatamaskiner, og y være den tida den siste meldinga skal forbli beskyttet (si, 30 år). La z være tida til du tror en tilstrekkelig stor kvantedatamaskin finnes. Dersom x + y > z, så bør du være bekymret allerede nå. Fremmede aktører samler antageligvis inn mye data allerede i dag, og vil forsøke å dekryptere så snart de kan.

Vi vet ikke når (eller hvis) tilstrekkelig store kvantedatamaskiner vil bli tilgjengelige. For å være på den sikre siden må vi legge til grunn at de kan komme i løpet av noen tiår. Kryptologer har derfor tatt utfordringen om å lage kvantesikker kryptografi på alvor i mange år.

Det er mange ideer til hvordan man kan gjøre det, men jeg skal konsentrere meg om to av de mest sentrale. Legg merke til at disse problemene er grunnleggende forskjellige fra de som brukes i dagens kryptografi.

Kodebasert kryptografi

Omtrent alle digitale kanaler bruker en eller annen form for feilrettende kode. Det betyr at dersom forstyrrelser på linja underveis introduserer noen feil, så kan mottakeren likevel rette dem opp. Enkelt sagt blir meningen kjent fra konteksten. En måte å oppnå det på er ved å multiplisere meldingen med ei spesiell matrise, som legger til noe ekstrainformasjon. For å dekode må man blant annet å multiplisere med ei tilsvarende matrise. Dette systemet er ikke i seg selv ment å gi sikkerhet mot utspekulerte angripere, og all informasjon om koden er kjent for alle involverte.

Kodebasert kryptografi holder disse matrisene hemmelige, og multipliserer kodingsmatrisa med to tilfeldige (men riktig strukturerte) matriser, slik at nøkkelinformasjonen blir ugjenkjennelig. For å kryptere kan man da multiplisere meldinga med den forkledde matrisa, og legge til noen tilfeldige feil. For den som lytter på linja ser sluttresultatet ut som en helt tilfeldig vektor.

For de som kan mer matematikk: La G være kodingsmatrisa for en Goppa-kode som kan rette t feil, la S være en inverterbar matrise, og la P være en permutasjonsmatrise. Sett G’ = SGP som den offentlige nøkkelen. For å kryptere beregner man c = mSGP + z, der m er en radvektor som representerer meldinga, og z er en radvektor med inntil t feil.

Teknikken har vært kjent siden McEliece oppdaget den i 1978, og gitt de riktige valgene av underliggende feilrettende kode er det hittil ingen kjente effektive angrep. Kjøretidene er også gode, men dessverre blir nøklene svært store. McEliece-kryptosystemet var derfor regnet som uinteressant inntil nylig.

Gitterbasert kryptografi

Se for deg et fiskegarn. Når du strekker ut garnet vil rutene endre form fra å være nesten flate, til å bli nær kvadratiske. Kryssene mellom trådene utgjør en gitterstruktur, der du i prinsippet kan starte et vilkårlig sted, og telle deg opp 15 kryss den ene veien, og 10 kryss den andre, og komme fram til et bestemt kryss. 

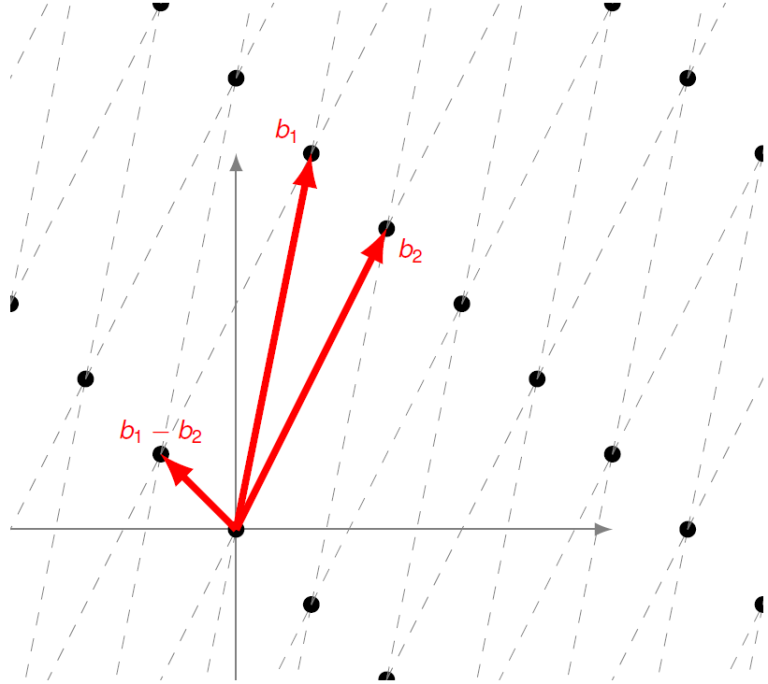
Et matematisk gitter er mye av det samme: Vi starter med en samling av vektorer. Den som kjenner lineæralgebra vet at en basisen vil spenne ut et vektorrom: hvert eneste punkt i rommet kan uttrykkes ved hjelp av en lineærkombinasjon av basisvektorene. Vi kan lage et gitter ved å lage kombinasjoner av de samme basisvektorene, men denne gangen tillater vi bare heltallskoeffisienter.

Ajtai foreslo i 1996 to vanskelige problemer på slike gitre.

• Gitt basisen og et tilfeldig punkt i vektorrommet, finn det nærmeste gitterpunktet, uttrykt ved hjelp av basisen.
• Gitt basisen, finn det korteste gitterpunktet.

Disse problemene er enkle dersom basisen består av vektorer som er nær ved å stå vinkelrett på hverandre («ortogonal», eller kvadratiske ruter i fiskegarnet), men blir vanskeligere dersom rutene er veldig skjeve.

Matematikk: Dersom du som kjenner lineæralgebra vil du umiddelbart foreslå å bruke Gram-Schmidt-prosessen til å gjøre basisen ortogonal, men det vil samtidig generere en helt ny gitterstruktur – akkurat som i fiskegarnet. Den mest kjente algoritmen for å forsøke å gjøre en gitterbasis mer ortogonal er LLL-algoritmen, som er en av grunnene til at Lovász fikk Abelprisen i 2021, og selv den gir oss ikke særlig nøyaktige resultater.

Et fiskegarn har bare to dimensjoner, mens gitrene vi bruker i kryptografi gjerne kan være tusendimensjonale. Den som til nå måtte ha greid å danne seg et bilde i hodet av hvordan dette ser ut har antageligvis mistet det nå.

Ajtais problemer er enkle å studere, men vanskelige å bygge kryptografi på. Regev viste i 2005 at dersom man lager et lineært ligningssystem, og legger til en liten feilvektor, så vil det normalt være like vanskelig som de vanskeligste av gitter-problemene. Dette kalles Learning with errors-problemet (LWE).

Mer matematikk: La Ax = b være et (muligens overdeterminert) lineært ligningssystem over en endelig kropp. Dette vet vi at vi kan løse effektivt. Om vi imidlertid velger en vektor e fra en smal, diskret Gauss-fordeling om 0, og nå betrakter ligningssystemet Ax + e = b, og holder x og e hemmelig, så vil en gjennomsnittlig instans av dette være like vanskelig som de vanskeligste, og de er igjen like vanskelige som de vanskeligste instansene av gitter-problemene.

Det er mye enklere å lage kryptografi fra et lineært ligningssystem, og vi kan bruke vesentlig lavere dimensjoner enn med McEliece. Det gir mindre nøkler.

Vi kan lage enda mindre nøkler ved å lage gitteret over en mer innholdsrik algebraisk struktur. I første omgang brukte vi et rent vektorrom. Vi kan også generere dette vektorrommet basert på det som kalles en syklotomisk ring, og få det som kalles Ring LWE (RLWE). Nøklene blir da enda mindre, men slike strukturerte gitre har mer informasjon som potensielt kan utnyttes i angrep mot systemet.

Standardisering og myndighetsanbefalinger

I 2016 startet NIST en prosess for å standardisere erstatninger for Diffie-Hellman og signaturer med tilsvarende mekanismer basert på kvantesikre teknikker. NIST ba om forslag fra forslag fra alle verdens kryptologer, og da støvet hadde lagt seg satt de igjen med 69 forslag som ble postet offentlig. Mange av disse ble angrepet mer eller mindre umiddelbart, men i 2022 satt NIST igjen med fire som de annonserte at de ville standardisere: CRYSTALS-Kyber for nøkkelutveksling, og CRYSTALS-Dilithium, Falcon og SPHINCS+ for signaturer. I tillegg har de også en liste over algoritmer de vil vurdere å standardisere dersom det kommer vesentlig ny informasjon, blant annet Classic McEliece.

De tre første algoritmene er basert varianter av strukturerte gitre. SPHINCS+ er basert på teknikker vi ikke har omtalt her, mens Classic McEliece naturlig nok er basert på McElieces opprinnelige algoritme.

NISTs standarder vil bli brukt til kommersielle formål, og spesielt på Internett. Algoritmene vil på sikt antageligvis erstatte de vi bruker i dag, selv om de den første tiden ofte vil bli brukt parallelt for å få sikkerheten fra begge. De store aktørene på Internett, som Google, Facebook og Cloudflare, er klare til å rulle ut kvantesikker kryptografi så snart standardene er ferdigstilte, og nylig ble det også annonsert at den sikre meldingstjenesten Signal er klar til å gå over til kvantesikker nøkkelutveksling. 

Like etter NISTs annonsering, offentliggjorde NSA at de vil godkjenne Kyber og Dilithium for amerikansk gradert data, helt opp til TOP SECRET. Nato og Norge har ikke bestemt seg ennå, men selv regner jeg med at vi vil få beslutninger som gir interoperabilitet i hele Nato.

BSI i Tyskland er derimot uenig med USA og NSA. De anbefaler forslaget FrodoKEM (basert på LWE i stedet for varianter av RLWE, «Frodo: Take off the ring!») og Classic McEliece. Det blir spennende å se om de vil omgjøre anbefalingen sin.

Ikke-løsninga: Kvantekryptografi

På tampen må vi snakke litt om elefanten i rommet: Quantum Key Distribution (QKD). Den vanligste ideen er fra Bennett og Brassard (1984), som regel bare omtalt som BB84. Ideen er at den ene parten koder et foton i en av fire tilstander, men der to og to tilstander henger sammen parvis. Fysikken er slik at mottakeren må velge et par på forhånd, og så forsøke å lese av fotonet. Dersom mottakeren valgte feil, så vil forsøket på å lese av tilstanden til fotonet endre tilstanden, og avlesingen blir helt tilfeldig.

Når mottakeren er ferdig med å lese, sender hen sine valg til avsenderen over en vanlig («klassisk») kanal, og de finner i fellesskap ut hvor de valgte samme par. Derfra er det videre mulig å komme fram til en felles hemmelighet, som kan brukes i symmetrisk kryptografi. Fysikken garanterer at dersom noen forsøker å avlytte kvantekanalen, så vil de statistisk sett ødelegge halvparten av signalet, og dermed nøkkelen. Uten en fungerende nøkkel, er det heller ingen data man kan dekryptere.

Fysikerne er veldig fornøyde med denne løsningen, fordi den – gitt en perfekt implementasjon – er umulig å knekke, og det er garantert av naturlovene. Kyber, Dilithium, og de andre eksemplene over er derimot avhengig av antagelser i matematikk, og det kan dukke opp noen som beviser at antagelsen er feil.

Det er likevel flere utfordringer med QKD. Den første er at vi trenger en separat infrastruktur, og som ikke kan inneholde signalforsterkning eller ruting. Det betyr fiberkabler eller luftlinje direkte mellom punktene. Noen stater ser på muligheten til å gjøre dette mellom bakken og en satellitt, og bruker da satellitten som en tiltrodd tredjepart.

Fysikken garanterer at nøkkelutvekslinga er sikker mot passive avlyttere, men vi kryptologer stiller strengere krav: Vi ønsker sikkerhet også dersom det er en aktiv motstander. Vi antar at motstanderen eier og kontrollerer kommunikasjonslinja. En angriper mot BB84 vil dermed bare klippe fiberkabelen i to, og utgi seg for å være den andre på hver side.

Den andre utfordringen er dermed at man er avhengig av at den klassiske kanalen har en mekanisme for å ivareta autentisitet, også mot en kvantedatamaskin. For å gjøre det trenger du for eksempel Dilithium-signaturer, men da er sikkerheten igjen avhengig av de samme matematiske antagelsene som fysikerne ville unngå.

Det er enklere å garantere at ingen sitter på linja dersom du sikter direkte på en satellitt. Skjønt, for de fleste av oss er det billigere å sende litt matematikk over den infrastrukturen vi har nå, heller enn å skyte opp en dedikert satellitt, og bare bruke egnet mottakerutstyr i friluft. Dette synet deles også offentlig av sikkerhetsmyndighetene i flere store land (USA, Storbritannia, Frankrike og Tyskland).

Så, går verden under?

Det er i dag noe diskusjon rundt hvor farlig Y2K-problemet egentlig var, men for denne fortellingens skyld kan vi legge til grunn at det gikk bra fordi noen gjorde den jobben som måtte gjøres. Det var ikke gratis, men verden gikk jo ikke under. 

Det kommer til å gå bra denne gangen også. NIST-standardene er snart ferdige, de store internett-aktørene er klare til å bruke dem, og kvantesikre algoritmer er på god vei til å bli godkjent for sikkerhetsgraderte anvendelser. Det er mye hardt arbeid som gjenstår, men verden vil ikke gå under, heller ikke denne gangen.